Name:____________
LAB 2
GEO 302C Climate: Past, Present and Future
BRING A
CALCULATOR TO CLASS!
Radiative Equilibrium and Forcing – The Ins and Outs
(see page 21 of your textbook; notice that there are some slight differences in the values used here.)
Definitions:
Blackbody: A blackbody is a hypothetical body (a coherent mass of any material) comprising a sufficient number of molecules absorbing and emitting electromagnetic radiation in all parts of the electromagnetic spectrum so that
· all incident radiation is completely absorbed (hence the term black), and
· in all wavelength bands and all directions the maximum possible emission is realized.
Solar radiation: Solar radiation is comprised of electromagnetic waves having magnetic and electrical properties. They do not need molecules to propagate them. In a vacuum, they travel at a constant speed of nearly 300,000 km (186,000 mi) per second – the speed of light. Solar radiation releases "heat" energy when it is absorbed by an object; the energy emitted from earth into space is in the form of infrared energy. Over the Earth as a whole, outgoing infrared energy equals incoming solar energy according to the Law of Conservation of Energy.
Albedo: The albedo of a planet is defined as the ratio of reflected solar radiation to incoming solar radiation. Snow has a high albedo, hence, a greater capacity to reflect light than say, a woodland forest, or a rocky desert.
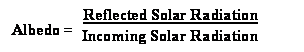
Case 1: Blackbody Earth
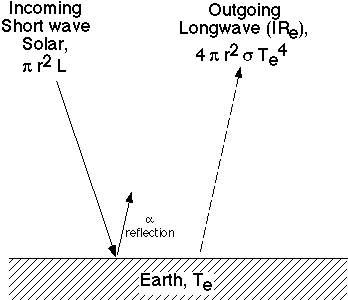
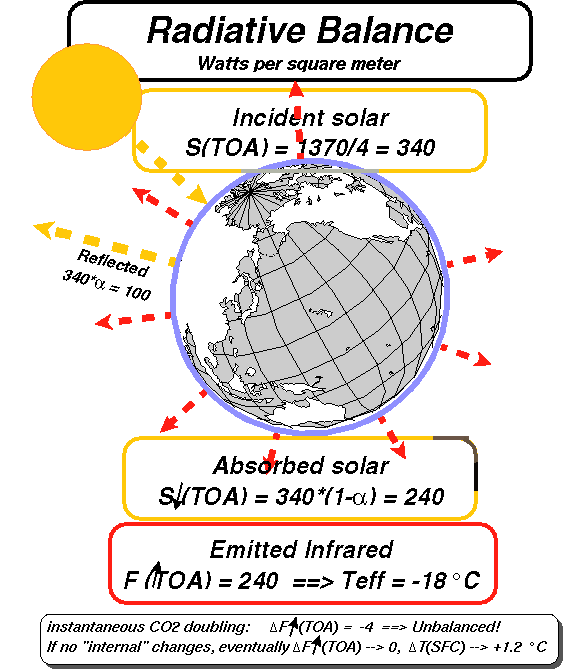
Consider a spherical planet “Earth” with no atmosphere. Energy from the Sun (solar radiation) pours down onto the Earth, a portion of the solar radiation being reflected back to space, and a remainder absorbed by the Earth.
The amount of solar energy absorbed by the Earth is given by
Flux
In = (1-a) pr2S
where:
a = albedo (reflectivity)
S = intensity of sunshine (the solar constant), 1367 W/m2
r = radius of a circle (the Earth intercepting Sunlight), 6,371,000 meters
pr2 = the area of the circle onto which the sun’s radiation falls
Assuming the “Earth” is a blackbody, the Stefan-Boltzmann law describes that the rate of energy being lost by outgoing infrared (IR) energy as a function of surface temperature, by
Flux
Out = 4pr2 sTe4
Where:
s = Stefan-Boltzmann constant, 5.67 x 10-8 W/m2/K4
Te = Temperature of the Earth’s surface
4pr2 = the surface area of a sphere (the Earth emitting infrared radiation during the day and at night)
Since the radiation flux in must equal the flux out, we can write
(1-a) pr2S = 4pr2 sTe4
and simplify this to
S(1-a)/4 = sTe4
Problems:
1. Express your answers in degrees Kelvin (K)
a) Calculate Earth’s equilibrium temperature Te for an average albedo of 0.33. Why is the temperature lower/higher than the observed average temperature of about 15°C or 288 K? ? Answer: 251 K, -21 C or -7 F, this is the top of the atmosphere it is warmer at the surface.
b)
Calculate the Earth’s equilibrium temperature Te during a
glacial period, where albedo = 0.75. Answer: 212.4
K, -60.5 C or -104 F Brrrr!
2. Refer to Table 2.1 on page 23 (Typical Albedos of Various Surfaces) of your textbook or from other sources (e.g., websites), calculate reflected energy out (i.e., αS) for the following, and the corresponding :
a) average earth
b) equatorial marine environment
c) the
d) alpine forest
e)
Bonus:
f)
White Sands,
g) What
would you guess for the typical range of albedo values for
3. Refer to the following website to complete entries on the table corresponding to Temperature with greenhouse effect and temperature without greenhouse effect using the following website:
http://paos.colorado.edu/~fasullo/1060/resources/0DModel.html
Please put your answers in the following table. Notice that
the solar constant = 1367 W/m2
Surface |
Albedo Value |
Incident Light |
Reflected Light |
Temperature Without Greenhouse (degree C) |
Temperature With Greenhouse (degree C) |
|
10 |
1367 |
136.7 |
-1.46 |
31.54 |
|
|
b) Equatorial Marine |
5 |
1367 |
68.35 |
2.23 |
35.23 |
|
c) The |
40 |
1367 |
546.8 |
-27.64 |
5.36 |
|
d) Alpine |
15 |
1367 |
205.05 |
-5.31 |
27.69 |
|
e) |
80 |
1367 |
1093.6 |
-86.57 |
-53.57 |
|
f) White Sands, NM |
50 |
1367 |
683.5 |
-38.57 |
-5.57 |
|
g) |
10 |
1367 |
136.7 |
-1.46 |
31.54 |
For Austin Texas you are allowed
to use any albedo value so long as you justify it and
your justification is consistent with you numbers
4. What trends do you observe in the above
table?
Getting about 32-33
degrees C of warming from the atmosphere. Temperature decreases with albedo, not quite linearly.
Greenhouse gasses help keep the planet warm, but albedo
can override their effect.
5.
Thought Questions:
Having understood the Sun’s incoming radiant energy, its reflectance back to space, and the dependency of reflected light on the albedo of the planet,
a) Would you expect the temperature of an ice-covered planet to increase or decrease over time? Why? What would be the result of this trend?
Thinking of albedo
alone, we would expect the temperature to decrease. Flux out would decrease until it reached a
new equilibrium. Ice would grow for some
time. I will also accept more risk
taking answers in which they try to indicate more complicated feedback loops.
b) Give some brief reasons other than the albedo as to why the Earth’s mean temperatures fluctuate through time. How is the Earth able to recover from extensive periods of glaciation or greenhouse conditions? A full treatise on the dynamics of Earth’s climate is not necessary, just a few brief observations taken from readings and lectures as to why the “Blackbody Earth” is not a complete picture.
Solar input and albedo are not everything,
they control only the First order climate.
We talk about the atmosphere and the gasses and the land cover. Think about equatorial oceans vs. oceans at
high latitudes! The objective of this
question is to initiate brainstorming about what it would take to change the
earth’s climate from an icehouse to a greenhouse. The proponents of Snowball earth