CHEMICAL THERMODYNAMICS

CHEMICAL THERMODYNAMICS

Definitions: (From Smith, 1982, and Anderson and Crerar, 1994)

Thermodynamics: Energy differences and transfers between systems.

Systems:

Isolated system: "have walls or boundaries that are rigid, do not permit transfer of mechanical energy, perfectly insulating, and impermeable. The have a constant energy and mass content.

Adiabatic systems: Perfectly insulated systems.

Closed systems: have walls that allow transfer of energy in or out of the system but are impervious to matter. They contain a fixed mass and composition, but variable energy.

Open Systems: have walls that allow transfer of both energy and matter to and from the system.

Simple Systems: Contain no interior walls.

Composite system: Two or more simple systems, and thus contain internal walls.

Equilibrium:

"A system at equilibrium has none of its properties changing with time. A system at equilibrium will return to that state after being disturbed.

State Variables:

Variables that define the state of a system. Extensive variables are proportional to the quantity of matter being considered (V, total Cp). Intensive variables are independent of quantity (concentration, viscosity, density, molar Cp)

Work (w): "The transfer of energy from one mechanical system to another. It is always completely convertible to the lifting of a weight". "The energy that flows across a system boundary in response to a force moving through a distance (such as happens when a system changes volume".

Heat (q): "The transfer of energy that results from temperature differences". "The energy that flow across a system boundary in response to a temperature gradient." "that part of any energy transfer that is not accounted for by mechanical work (FxD)." q=DU-w

Heat Capacity: The relation between heat transferred to a body and the change in T.

Enthalpy: The increase in enthalpy of a system is equal to the heat absorbed at constant pressure, assuming the system does only PV work.

Entropy: A measure of the loss of capacity of the system to do work.

Zeroth Law: "Two bodies in thermal equilibrium with a third are in thermal equilibrium with each other" (Basis of the concept of temperature)

First Law: "The alegraic sum of all energy changes in and isolated system is zero" (Conservation of energy). Energy can be converted from one form to another but cannot be created or destroyed. DU=q+w. This is based only on observation

Second Law: "Spontaneous changes are those which, if carried out under the proper conditions, can be made to do work. If carried out reversibly they yield a maximum amount of work. In natural processes, maximum work is never obtained.

Basic Principles

Thermodynamics is the study of energy in systems, and the distribution of energy among components. In chemical systems, it is the study of chemical potential, reaction potential, reaction direction, and reaction extent

First Law of Thermodynamics:

dU=dq + dw

where U is the internal energy, q is the heat transferred to a system from the surroundings, and w is the work done on a system by the surroundings.

"The change in the internal energy, dE, is the sum of the heat transferred to the system, dq, and the work done on the system, dw. This is the energy conservation principle for a system" (Stumm and Morgan, 1981, p. 17). For a finite change:

DU=q + w

Work and Reversible reactions.:

"Work is the transfer of energy from one mechanical system to another. It is always completely convertible to the lifting of a weight.
Work done on a system is positive, and work done by the system as negative. An example of work by the system is the expansion of a cylinder against the atmosphere.

For a system doing only PV work:

dU = dq + dw

dU = dq - PdV

where PdV is the reversible expansion work done on the system by the surroundings.

An analog of a system doing no work would be a sled going down a hill. The reaction is spontaneous, and potential energy is eventually converted to heat due to friction (w=0, dU = dq. The reaction proceeds until the potential energy minima is reached, i.e., the bottom of the hill. The reverse reaction is not spontaneous.

An analog for a system doing work would be if one attached an object to the sled over a pulley, where the mass of the object M₂ < M₁, the mass of the sled and driver. As the sled goes down hill, the object is pulled upward, and work is done (dU = dq + w; w = M₂gdh).
As the mass of the object M₂ increases, more work is accomplished, until M₁ is only infinitesimally greater than M₂, and the maximum amount of work can be accomplished as the sled moves infinitely slowly, and only an infinitesimal amount of energy is required to reverse the process.

Second Law of Thermodynamics

The second law is concerned with entropy (S), which is that part of the total energy of the system that is not available to do useful work. Entropy is a fundamental variable in thermodynamics, and is responsible for such phenomena as molecular diffusion. For an interesting view of entropy, check out the movies at The U.C. San Diego.

Statement One: "The total entropy change of the closed system is dSsys and is the sum of changes inside the system, dSint, and entropy transferred to the system from its surroundings, dSsur.
dSsys= dSint + dSsur

dSsur = dq/T

For a reversible process or equilibrium state of the system, the second law states that the internal entropy change is zero:

dSint = 0

For a spontaneous or natural process in the system

dSint > 0

So for any spontaneous natural process

dSsys > dq/T

The internal entropy change for a closed system is zero at equilibrium and positive for a spontaneous process. The heat transferred to a closed system, divided by T, is equal to or less than the entropy increase for any possible process. The entropy of an isolated system increases in any spontaneous process and attains a maximum for any reversible process. (Stumm and Morgan, p. 19).

Free Energy

The Gibbs Free energy is that portion of the total system energy that is available for useful work.

For most cases in water chemistry, The system is closed to the addition and removal of matter, but open to the transfer of energy.

The system is at constant temperature and pressure, does only PV work, with P constant, so only expansion work is done:

dw=-PdV

At equilibrium, and with fixed composition (no addition of material):

dq = TdS(sys)

dU = TdS - PdV

So the internal energy is a function of entropy and volume. Another expression for total system energy is Enthalpy (H):

H = U + PV

dH = dU + PdV

When T and P are constant, we can use Gibbs expression for free energy

dG = dU + PdV - TdS

dG = dH - TodS

Where:

G = Gibbs free energy, kcal/mol

T = absolute temperature, oK

S = entropy, cal/oK

H = enthalpy, kcal/mol

This equation tells us if a reaction will happen, and in what direction.

a) Enthalpy: the total energy content of acompound (dH = dU+PdV) in kJ/mol; .

b) Free Energy: That part of the total energy that is available to perform "useful work", that is, other than PV work, such as electrical work, in kJ/mol.

Entropy: the degree of disorder of a system. The product TS is that part of the free energy which is NOT available for useful work, in joules/^oK.

Heat Capacity:

Heat capacity is defined as the change in temperature of a system with a change of heat transferred to the system:

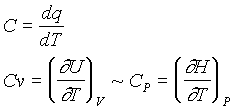
Heat capacity can be measured directly by calorimetry (at constant pressure), and can provide information on enthalpy for a closed-system process.

Law of Mass Action:

The driving force of a reaction is related to the concentrations of reactants and products.
aA + bB ---> cC + dD

The ratio of products to reactants is expressed by the equation:

At equilibrium this ratio is equal to the equilibrium constant, K.

Equilibrium

For a closed system at constant pressure and constant temperature, the criterion for equilibrium is that the total free energy of the system (GT) is a minimum.

If we were to add A and B to a reaction vessel and calculate total free energy as a function of reaction extent ( x ), we would get:

The TOTAL FREE ENERGY is the sum of the free energies of each component.

GT = nAGA + nBGB + nCGC + nDGD

Where Gi = Free energy / mole of i

ni = number of moles of i

For a reaction proceeding in incremental amounts toward equilibrium, the change in GT is proportional to dG, where

DG = (SuiGi)products - (SuiGi)reactants

Where: ui = the stoichiometric coefficient

Gi= the free energy per mole

Applying to our base equation: DG = DH - T�DS (at constant T,P)

a) DG < 0, and GT decreases as the reaction proceeds, the reaction is spontaneous.

b) DG = 0, the reaction is at equilibrium, and GT is at a minimum

c) dG > 0, the reaction is not spontaneous as written, but proceeds in the opposite direction.

Values of DG for a reaction can predict whether or not reactions are possible. To calculate DG for the general mass reaction we use the relationship:

DG = DG� + RT lnQ

Where: DG� = (SuiG�i)products - (SuiG�i)reactants

_

G�i = free energy per mole at standard state.

Free energy of formation:

To calculate the equilibrium state before the reactions occurs, it is necessary to calculate the chemical potential of each component, but it is only possible to measure change in free energy.
Therefore, the standard free energy of formation is defined as the change in free energy to form the compound from its constituent elements, which are arbitrarily assigned a value of 0.
This can be used to determine the overall standard free energy change for the reaction, dGr� from the free energies of formation:

Free Energy of Reaction:

The free energy of the reaction is equal to the sum of the free energies of formation of the products minus the sum of the free energies of the reactants at standard state:

DG� = (SuiG�f,i)products - (SuiG�f,i)reactants

Further, we can relate the free energy of a single substance at a state other than standard to its free energy of formation at standard state by the expression:

Gi = DG�f,i + RT ln {i}

Where {i} is the effective concentration or activity of species I

Example Calcium carbonate:

Cgraphite + 3/2 O2 + Ca ---> Calcite DG�f = -269.78 kcal/mol

Cgraphite + 3/2 O2 + Ca ----> Calcite	DG�f = -269.78 kcal/mol
H+ ------> H+	D G�f = 0
Ca-----> Ca++	DG�f = -132.18
H+ + C + 3/2 O2 ------> HCO3-	DG�f = -140.31

DG� = (Sv_iG�_f,i)_products- (Sv_iG�_f,i)_reactants
CaCO3 + H+ --------> Ca++ + HCO3- G�r = -2.71

Reacting 1 mole of acid with one mole of calcite releases free energy, so the reaction is spontaneous.

Activity vs. Concentration

The value of the activity of a substance is dependent on the choice of standard state conditions, or the conditions that result in unit activity.

For ions and molecules in solution, (i) is related to the molar concentration [i], by (i) = g_i[i], where g is the activity coefficient. As the solution becomes dilute g_i approaches 1.

For the solvent in a solution (i) = g_iXi, where Xi is the mole fraction. As the solution becomes more dilute, g_i approaches 1. The activity generally is assumed to be 1 for the dilute solutions of concern here.

For pure solids or liquids in equilibrium with a solution, (i) = 1.

For gases in equilibrium with a solution, (i) = g_i Piwhere Pi = is the partial pressure of the gas in atmospheres. As the total pressure decreases, g_i approaches 1. When reactions take place at atmospheric pressure, the activity of a gas can be approximated closely by its partial pressure.

6 For mixtures of liquids, (i) = Xi

Returning to the example:

DG = [DG�f,HCO3 + RTln{HCO3-} + DG�f,Ca++ + RTln{Ca++}] –

Collecting Terms:

- [DG�f,H+ + RTln{H+} + DG�f,CaCO3 + RTln(CaCO3)]

W can state

and since the activity of a solid is unity:

DG = DG� + RT ln Q

When the value of Q is identical to that of the equilibrium constant K, and DG = 0,

0= DG� + RT ln K; DG�= -RT ln K

When not at equilibrium, substituting we can get

DG = -RT ln K + RTlnQ

= +RT ln Q/K

when Q/K>1, not spontaneous

Q/K =1, equilibrium

Q/K < 1, spontaneous

Example 3-1, S&J

Determine the equilibrium constant for the dissociation of water at 25�C:

H2O <----> H+ + OH-

1. Find the DGf of the reactants and products:

Species DG�f,

H2O -56.69

H+ 0

OH- -37.60

2. Sum the energies of formation to get a standard free energy of reaction

DG� = (1)(0) + (1)(-37.6) - (1)(-56.69) = 19.09 kcal

19.09 = -RTlnK

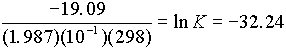
K = [H+]{OH-] = 10-14

3. Use reaction rates to find equilibrium:

H+ + OH- <----> H2O

k-1

with k1 = 1.4x1011 liter/mole sec

k2 = 2.5x10-5 /sec

� These are the fastest rates known in aqueous solutions, where the reaction is essentially instantaneous, with the overall rate limited by the rate of diffusion of reactants.

� Since the reaction is elementary, we can write:

Forward rate = k1[H+][OH-]

Reverse rate = k2[H2O]

� Since at equilibrium, the forward rate = reverse rate:

k1[H+][OH-] = k2[H2O]

k2[H2O]/k1 = [H+][OH-] (mole2/liter2)

� Substituting for k's, and using 5.5 moles/l for water concentration: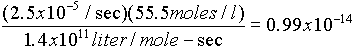

Chemical Potential

a) The chemical potential is the molar free energy G/ni, and describes the system for components not in the standard state, especially for components at concentrations other than 1 molar.

mi = (dGi/dni)T,P

b) Example: Multi Phase system:

1) When two or more phases coexist at equilibrium, the chemical potential of all components in the system must be identical in each phase

at equilibrium, mA = mB

� if mA is greater than mB, than some reaction will occur to bring the system to equilibrium, ie mA = mB, resulting in the release of energy (-DG). Usually, this means the transfer of some component i from A to B.

� Any combination of phases will do.

Temperature And Pressure Dependence OF K, G, H

The driving force of a reaction is DG, as an expression of useful work (non-PV work). This is comprised of 2 components, enthalpy and entropy. At equilibrium:

DG = DH - T�DS

So the magnitude and direction of the driving force depends on the magnitude and direction of H and S. Neither by themselves controls the reaction.

Enthalpy And The Temperature Dependence Of K

The enthalpy change of a chemical reaction (DH) is the amount of heat that is released or taken up during the course of the reaction.

a) Endothermic = positive DH

b) Exothermic = negative DH

DH can be expressed in terms of G, S, and T as: DH� = DG� + T� DS� and represents the TOTAL energy of the system, both usable and unusable. At equilibrium, DH=+T�DS

Similarly to DG�, DH� for a reaction can be calculated by:

DHo = S (DH�products) - S (DH�reactants)

Also similarly to DG�, the absolute value of DH� cannot be directly measured, and so the elements are assigned a value of 0, and then calculating the enthalpy of formation.

The standard enthalpy change DH� is used to determine the effect of temperature on the position of equilibrium. The basic equation is:

dG = - SdT + VdP

Which at constant pressure can be written as

so the change in free energy with temperature is related to entropy. For a finite change in state:

divide through by T2:

and

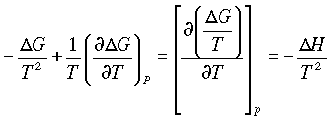
giving the Gibbs-Helmholtz equations

By differentiating the equation: DG� = -RT lnK, we obtain

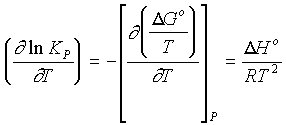
an equation called the Van't Hoff Isochore

Since by definition the standard system is at 1 atm, and DG� and DH� are not function of pressure, we can write the full differential thus:

So the equilibrium constant varies with temperature as a function of the Enthalpy of the system (Assuming dH does not vary with temperature.).

If we assume that -DH� is independent of temperature, integration of the equation yields:

or

Plotting log K against 1/T results in a line whose slope is --DH�/2.3R

a) For an exothermic reaction, K must decrease as the temperature increases....

Ideal And Non Ideal Solutions

Chemical Potentials In Phases:

Chemical Potential: G = m = m(T,P)

For pure solids and pure liquids the chemical potential is the molar free energy G bar, and is a function of T and P only.

by convention we refer to the chemical potential of a component at 1 atm as m�, so

m = m�(T)

2.Chemical potential of an ideal gas.

� For n moles of pure gas at constant temperature

dG = VdP

� From the ideal gas law:

V = nRT1/P

dG = nRT dP/P

dG = nRTdlnP

� Integrating from a standard pressure P� to a pressure P yields

G-G�=nRTln P/P�

Dividing by n

G/n - G�/n = RTln P/P�

� Since the chemical potential for a one-component phase is G/n:

m(g) - m�(g) = RTln P/P�

When P = P�, m(g) = m�(g), or

mi(g) = m�i(g) + RT lnP/P�

If P� = 1

mi(g) = m�i(g) + RT lnP

and in an ideal gas mixture:

mi(g) = m�i(g) + RT lnPi

� where the value of m at 1 atm is m� standard state, and Pi is the partial pressure of component i. If xi is the more fraction of component i: Pi = XiP, leading to:

mi(g) = m�i(g) + RT lnP + RTln Xi

Chemical potentials in ideal solutions:

a) This closely follows ideal gas mixtures: (159)

mi(sol) = m�i(sol) + RT lnXi

Where: Xi = the mole fraction of i in solution

For a solution of component i in equilibrium with a vapor phase, the general criterion of equilibrium dG = 0, yields as the condition of 2-phase equilibrium

mi(sol) = mi(g)

Assuming the vapor phase is an ideal gas mixture, we get:

mi(sol) + RT ln Xi = m�i(g) + RT lnPi

Rearranging

1) This equation states that the vapor pressure of component i is proportional to its mole fraction in a solution behaving ideally. This is the base equation for Raoults and Henrys law.:

Raoult's Law:

The ideal gas vapor pressure of an ideal solution component is equal to the vapor pressure of the pure liquid component multiplied by the mole fraction of the component in the solution, or:

Pi = XiP�i

where Pi is the partial pressure,

Xi is the mole fraction, and

P�i is the partial pressure of pure component i.

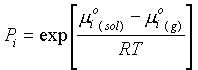
and when Xi = 1:

m�i(sol) = m�i(g) + RT lnP�i

Thus the standard state chemical potential for the ideal solution component depends on the ideal gas state and the convention that Xi =1 is the standard state for the component in solution.

--For real solutions, Raoult's law behavior is approached as Xi ---> 1.

Henry's Law:

For a dilute solution the ideal gas vapor pressure of a volatile solute is proportional to its mole fraction in the solution; that is, escaping tendency of the solute molecule is proportional to their mole fraction, ie:

Pi = KiXi

This means that Ki is the slope of the plot of Pi vs Xi for sufficiently dilute solutions, or where solute-solute interactions are negligible.. So:

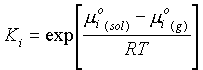For real solutions, Henry's law behavior is approached as Xi approaches 0.

Important: m�i(sol) for a Henrys law solute reflects the properties of a dilute solution, and for a Raoults law component it reflects the properties of a pure component, in other words, the solvent.

Nonideal Behavior Of Ions And Molecules In Soluitons:

For Real Solutions:

1) The term activity is used for idealized concentration, vs actual concentration:

mi = m�i + RT lnai

and

ai = giXi

giving the chemical potential in a real solution:

mi = m�i + RTlngiXi

and

mi = m�i + RTlngi+ RTlnXi

Where the expression RTlngi is the partial molar free energy of the interactions that occur in nonideal mixtures.

Volatile Solution Components

If mi(sol) = mi(g) then:

mi(sol) + lngiXi = m�i(g) + RT ln Pigfi

If the pressure of the vapor is low enough so that gfi = 1, the solution-phase activity coefficient is:

g1 = P1/P�1

a1 = g1X1 = P1/P�1

so the activity of the solvent is described by the ratio of its vapor pressure over a solution to the vapor pressure of pure solvent. For an ideal solution the activity is precisely Xi and is described by Raoults law, and gi = 1.

For real solutions, activity coefficients are not unity and vary with composition.

Ionic Strength Effects On Equilibrium:

In very dilute aqueous solutions, ions behave independently of one another and we assume that activity coefficients of ions are unity.

However, as the concentration of ions in solution increases, electrostatic interactions between the ions also increase, and the activity of ions becomes somewhat less than their measured or analytical concentration:

ai = gi Xi or {i} = g[i]

--The activity coefficient becomes less than one and the chemical equilibrium is affected, forcing the rewriting of the mass action equation to:

But from a purely thermodynamic point of view there is no way in which the activity of a single ion can be measured without introducing non thermodynamic assumptions, i.e. Single ion activity coefficients

To calculate the activity coefficients of solutes in real solutions, the effects of actual solute mixture must be taken into account, ie, non-infinite dilution.

The generalized expression of these effects is the ionic strength, defined as:

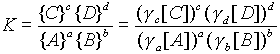
This describes the magnitude of the interionic effects, or the intensity of the electric field in a solution.

Example 3-6:

Compute the ionic strength of a solution containing the following concentration of ions:

[Ca2-] =10-4M, [CO32-] =10-5M, [HCO3-] =10-3M, [SO42-] =10-4M, [Na+] =10-3M

m = ([10-4 x 22]+[10-5x22]+10-3x12]+10-4x22]+[10-3x12])

m = 1.43x10-3

I ~ 2.5x10-5xTDS; I = 1.6x10-5 x specific Conductance

The specific expression of the electrostatic and interionic complexing effects resulting in the activity coefficient is derived using a choice of approximating equations.

DeBye-Huckel limiting law:

This is the simplest equation, and is good up only up to I = 0.005

� Based on the effect ionic interactions should have on free energy. In an ionic solution, positive ions will tend to have a cloud of negative ions around them, and negative ions a cloud of positive ions.

� If it is assumed that the ions are point charges, the interactions are entirely electrostatic, and the ions around any particular ion follow a Boltzmann distribution.

Extended DeBye-Huckel approximation of the DeBye-Huckel limiting law,

applicable for ionic strength I<0.1M

Where:

A = a constant that relates to the solvent, and varies with temperature. (A = 1.82 x 106(eT)-3/2, e = dielectric constant.)

A = 0.5 at 15�C; 0.509 at 25�C

B = a constant that relates to the solvent and varies with temperature. B=50.3(eT)-1/2

B = 0.326x108 at 15�C; and 0.328x108 at 25�C.

ai =a constant that relates to the diameter of the hydrated ion. For monovalent ions except H+ this is about 3-4 x 10-8

Zi = the charge of the ion

The Guntelberg approximation

plugs in the monovalent coefficients at 15�C:

This approximation is useful in solutions of mixed ions with varying charges, since the limiting law is not satisfactory with mixed charge types, and is useful up to I = 0.1.

Davies equation

This is best at higher ionic strengths; to about I = 0.5m

Electroneutrality:

� All solutions are charge balanced, with the meq of anions exactly balanced by the meq of cations. The standard equation is: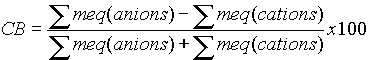

The usual QA cutoff is +/- 5% on the CB, or with the alternative equation, 10%. This is often exceeded with very dilute waters and brines.

Relation of ionic strength to TDS

m = 2.5 x 10-5 x TDS

m = 1.6 x 10-5 x specific conductance (mmho/cm)

Activity coefficients of nonelectrolytes in aqueous solutions:

This is not as well developed as for electrolytes, and is based on empirical equations such as

log g = ks m

For this equation, the salting-out coefficient ks must be experimentally determined, and is generally in the range of 0.01 - 0.15

nonionic solutes have activity coefficient of nearly 1 for I < 0.1

Example: dissolved oxygen in NaCl:

ks = 0.132
m = 0.05
log g = 0.132 x 0.05 = 0.0066
g = 1.02
so as the ionic strength increases, the activity coefficient increases.

REVIEW OF IMPORTANT EQUATIONS:

1. Mass Action aA + bB ---> cC + dD

2. Free Energy G = H - ToS

DG = (SuiGi)products - (SuiGi)reactants

DG = DH - T�DS (at constant T,P)

DG = DG� + RT lnQ

0 = DG� + RT ln K

or

DG�= -RT ln K

DG = -RT ln K + RTlnQ

= +RT ln Q/K

3. Temperature effects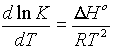

or

4. Gas Laws Raoult Pi = XiP�i

Hanks Pi = KiXi

5. Activity mi = m�i + RT lnai

and ai = giXi

6. Activity Coef. ai = gi Xi or {i} = g[i]

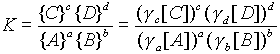
7.